
The last note is that from the equation (6) we have Let us derive other useful formulas for the segments x and y measures. To express z via the measures a and b of the legs only. It expresses the length of the altitude in the right triangle drawn from the right angle vertex to the hypotenuse. This formula is exactly what we are seeking for. Open the brackets and cancel the like terms.

Note that these expressions are rewritten equations (1) and (2). We getĭue to Pythagorean theorem for the right triangle ABC.Ĭomparing the equations (4) and (5), we get Let us add the equations (1) and (2) (both sides). Let us square the equation (3) (both sides). (2) (Pythagorean formula for the right triangle BDC), and (1) (Pythagorean formula for the right triangle ADC), Let us express x, y and z via known quantities: Now, we want to derive the formula expressing z via a, b and c. Let z be the length of the altitude drawn to the hypotenuse ( Figure 1). Let x and y be the measures of the segments the altitude cutsįigure 1. So, we can assume that not only the measures a and b are given,īut the measure c of the hypotenuse is known also. We can calculated the length of the hypotenuse by the More proofs of the Pythagorean Theorem under the topic Pythagorean Theorem of the section Geometry in this site.Ĭonsider the right triangle with the legs measures of a and b.Ĭalculate the length of the altitude drawn from the vertex of the right angle to the hypotenuse.įirst, knowing the legs measures a and b of the right triangle, For the proof of this theorem see the lessons The Pythagorean Theorem and The base for solving this kind of problems is the Pythagorean Theorem. This lesson focuses on calculating the length of the altitude drawn to the hypotenuse of the right triangle. So it's okay to have an altitude that is not inside your triangle.Altitude drawn to the hypotenuse of a right triangle If I look at the other two altitudes in this obtuse triangles, we're going to have one altitude going like that I'm going to have to extend that side as well and we'll drop down another altitude. Notice that I had to extend that opposite side. So if we pick this vertex, our opposite sides are over here but that opposite side doesn't continue to where this altitude will drop. So a third case is the obtuse triangle, and here is where I say to a line containing the opposite side. However if I pick my 90 degree angle as my vertex, then we'll be able to see that altitude inside the triangle. If I pick this vertex right here the altitude will just be that leg of the triangle. That's going to be that leg of the triangle. If we look at a right triangle over here we can see that if I pick this vertex right here, we already have an altitude drawn.

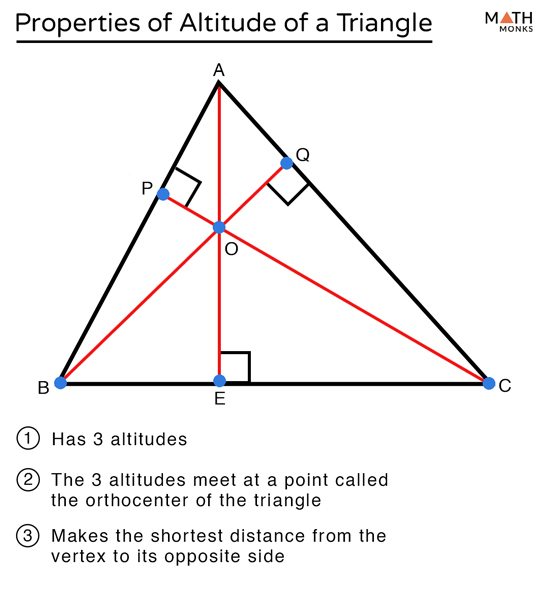
Notice that all three altitudes are inside the triangle. We would have two more altitudes, each of which would go perpendicular to the opposite side. So if I were to pick this top vertex right here, the altitude would go straight down perpendicular to the opposite side. So if we look at an acute triangle, there are going to be three altitudes, one form each vertex. It's not always to the opposite side and you're going to see why in a second here. So this definition is written very carefully. What we're talking about is a perpendicular segment, remember this symbol right here means perpendicular-I'm trying to get you used to seeing these symbols-from a vertex to a line containing the opposite side. When we're talking about triangles, there's a special segment three in each triangle called an "Altitude." So we're not talking about skiing here.


 0 kommentar(er)
0 kommentar(er)
